In unserer Welt, wo Zahlen jeden Aspekt des täglichen Lebens beeinflussen – von der Messung der Zeit über die Verwaltung finanzieller Mittel bis hin zur Einschätzung wissenschaftlicher Daten –, ist das Verständnis für grosse Zahlen für das mathematische Allgemeinwissen unerlässlich. Millionen, Milliarden und darüber hinaus sind nicht nur abstrakte Konzepte, sondern auch fundamentale Werkzeuge, um das moderne Leben zu navigieren.
Im Thema Mathematik kommen wir ständig mit solchen Grössenordnungen in Berührung, ob beim Lernen, Rechnen oder beim Analysieren von Daten. Eine Million beispielsweise, eine Zahl mit sechs Nullen, wird oft als Sprungbrett zu noch grösseren Zahlen wie der Milliarde (neun Nullen) oder der Billion (zwölf Nullen) genutzt.
| Name | Zahl | Anzahl der Nullen |
|---|---|---|
| Milliarde | 1 000 000 000 | 9 |
| 1 Billion | 1 000 000 000 000 | 12 |
| 1 Billiarde | 1 000 000 000 000 000 | 15 |
| 1 Trillion | 1 000 000 000 000 000 000 | 18 |
| 1 Trilliarde | 1 000 000 000 000 000 000 000 | 21 |
| 1 Quadrillion | 1 000 000 000 000 000 000 000 000 | 24 |
| 1 Quadrilliarde | 1 000 000 000 000 000 000 000 000 000 | 27 |
| 1 Quintillion | 1 000 000 000 000 000 000 000 000 000 000 | 30 |
| 1 Quintilliarde | 1 000 000 000 000 000 000 000 000 000 000 000 | 33 |
| 1 Sextillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 | 36 |
| 1 Sextilliarde | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 | 39 |
| 1 Septillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 42 |
| 1 Septilliarde | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 45 |
| 1 Oktillion | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 48 |
| 1 Oktilliarde | 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 | 51 |
Doch was ist eigentlich die grösste Zahl? Theoretisch sind Zahlen unendlich, und Mathematiker können immer eine Zahl finden, die eine Einheit grösser ist als die bisher grösste bekannte Zahl. Im praktischen Gebrauch jedoch wird häufig der Begriff "Googol" – eine 1, gefolgt von hundert Nullen – zitiert, um die Grösse unserer Vorstellungskraft zu verdeutlichen. Dies führt uns zu einer weiteren interessanten Frage: Wie können wir solche enormen Grössen verstehen und korrekt darstellen?
Suchst du nach einer Nachhilfe Mathematik Oberstufe? Superprof hat das passende Angebot für dich!
Grosse Zahlen schreiben und lesen
Das korrekte Schreiben und Lesen grosser Zahlen ist eine grundlegende Fähigkeit in der Mathematik und Voraussetzung dafür mit grossen Zahlen schriftlich zu rechnen. Um grosse Zahlen zu meistern, ist es essenziell, das Thema "Stellenwert" und "Stellenwerttafel" zu verstehen. Eine Million – die aus einer 1 mit sechs Nullen besteht – sollte als "1.000.000" geschrieben werden, um Klarheit in der Darstellung zu gewährleisten. Milliarden und Billionen folgen einem ähnlichen Schema, wobei eine Milliarde als "1.000.000.000" und eine Billion als "1.000.000.000.000" geschrieben wird.
Es gibt mehrere Möglichkeiten, grosse Zahlen wie beispielsweise eine Million darzustellen, um ihre Lesbarkeit zu verbessern. Die Nullen werden dabei in Dreiergruppen unterteilt:
Mit Leerzeichen getrennt: 1 000 000
Mit Punkten gegliedert: 1.000.000
In Wortform: eine Million
Abgekürzt mit Zahl: 1 Mio.
Beim Lesen dieser Zahlen ist es wichtig, die Zahlen in Gruppen zu teilen. Jede Gruppe repräsentiert Tausender, Hunderter oder Zehner, was das Lesen erleichtert. Zum Beispiel wird "123.456.789" als "einhundertdreiundzwanzig Millionen vierhundertsechsundfünfzigtausend siebenhundertneunundachtzig" gelesen.
Fragen? 🥴 Finde mit Superprof die passende Nachhilfe Mathematik Oberstufe!
Metrische Vorsätze für grosse Zahlen
Metrische Vorsätze erleichtern das Verständnis und die Handhabung grosser Zahlen in der Mathematik und im Alltag. Beginnend mit "Kilo" (tausend) über "Mega" (Million) und "Giga" (Milliarde) bis hin zu "Tera" (Billion), ermöglichen diese Präfixe es uns, mit enormen Grössenordnungen zu arbeiten, ohne ständig zahlreiche Nullen schreiben oder aussprechen zu müssen.
Beispielsweise repräsentiert ein Kilogramm tausend Gramm, während ein Gigabyte einer Milliarde Bytes entspricht. Diese Präfixe sind nicht nur in der Naturwissenschaft, sondern auch in der Technologie und Wirtschaft allgegenwärtig, wo sie zur Beschreibung von Datenvolumen, Frequenzen und Kapazitäten verwendet werden. In der Informatik beziehen sich Terabyte und Petabyte auf die Kapazität von Festplatten oder die Menge an generierten Daten, was das Stellen von Datenmengen, ihre Verwaltung und Analyse betrifft.
Das Erlernen und Verwenden dieser Präfixe ist daher unerlässlich, um die Ziffern und Potenzen grosser Zahlen effektiv zu bearbeiten und zu nutzen. Sie dienen als praktische Werkzeuge, um die Komplexität der Zahlen zu reduzieren und ihre Handhabung zu vereinfachen, was in vielen wissenschaftlichen und technologischen Bereichen entscheidend ist.
Finde Mathe Nachhilfe Zürich - mit einem Superprof kommst du schneller ans Ziel!
Verständnis für die Grössenordnung
Grosse Zahlen sind oft schwer zu fassen, doch ihre Visualisierung kann helfen, ein besseres Verständnis für ihre Dimensionen und das Thema zu entwickeln. Eine Million, zum Beispiel, ist eine Zahl, die wir häufig hören – sei es in Bezug auf Einwohnerzahlen, die Anzahl von Sternen im Himmel oder sogar die Zahl der Schritte, die man in einem Jahr geht. Eine Million zu visualisieren, könnte bedeuten, sich ein Fussballstadion vorzustellen, das zehnmal gefüllt ist, denn ein grosses Stadion fasst etwa 100.000 Zuschauer.
Noch anschaulicher wird es bei einer Milliarde. Um eine Milliarde zu visualisieren, könnte man sich vorstellen, dass man jeden Tag, für etwa 2,7 Jahre (über 1000 Tage), eine Million CHF ausgibt. Dies verdeutlicht die gewaltige Differenz zwischen einer Million und einer Milliarde, und zeigt, wie wichtig es ist, diese Grössenordnungen korrekt zu verstehen.
12 von 8 Menschen sind mit Mathe total überfordert.
Ein weiteres Beispiel ist die Verwendung von "Milliarden" in der Wissenschaft, wie etwa die Menge der Zellen in einem menschlichen Körper oder die Distanz zwischen Sternen in Lichtjahren. Solche Kontexte helfen, den Umgang mit Zahlen zu lernen und die Stellenwerte zu schätzen, was für das Fach Mathematik unerlässlich ist.
Im Alltag begegnen uns diese Zahlen in vielfältiger Weise, sei es durch die Anzahl von Bytes in Computern (Gigabytes, Terabytes) oder durch die Menschenmassen bei grossen Veranstaltungen. Auch im Mathe-Unterricht können grosse Zahlen in Textaufgaben immer wieder vorkommen. Die Visualisierung und das praktische Beispiel machen nicht nur den Stellenwert greifbar, sondern lehren uns auch, mit den Zahlen natürlich zu rechnen und sie zu verstehen.
Suchst du Mathe Nachhilfe Zug? Lass dir von einem unserer Superprofs weiterhelfen.
Wie viele Nullen hat eine Million?
Eine Million hat sechs Nullen. Diese einfache Tatsache ist ein grundlegender Bestandteil des mathematischen Verständnisses und spielt eine zentrale Rolle in der Stellenwerttafel, einem unverzichtbaren Werkzeug zum Erlernen und Vergleichen grosser Zahlen. Die Stellenwerttafel hilft dabei, jede Ziffer einer grossen Zahl in ihren entsprechenden Kontext zu setzen, von den Einerstellen rechts bis hin zu den Millionen und darüber hinaus auf der linken Seite.
hat sechs Nullen
Zum Beispiel wird die Zahl 1.000.000 in einer Stellenwerttafel so dargestellt, dass die '1' in der Spalte der Millionen steht und sechs Nullen folgen, die die Tausender, Hunderter, Zehner und Einer darstellen. Dieses System ermöglicht es nicht nur, grosse Zahlen wie Millionen, Milliarden oder sogar Billionen einfach zu verstehen, sondern auch, sie effektiv zu vergleichen. Durch das Vergleichen der Stellen kann man schnell erkennen, dass eine Milliarde (1.000.000.000) dreimal so viele Nullen hat wie eine Million.
Die grösste Zahl
In der Welt der Mathematik begegnen uns oft unvorstellbar grosse Zahlen, die unsere Vorstellungskraft herausfordern. Ein prominentes Beispiel ist der Googol, eine 1 gefolgt von hundert Nullen. Noch gewaltiger ist der Googolplex, der als 1 gefolgt von einem Googol an Nullen definiert ist. Diese Zahlen sind nicht nur mathematische Kuriositäten, sondern haben auch praktische Anwendungen in der Theorie grosser Zahlen und in der Informatik, besonders im Bereich der Kryptographie und Algorithmentheorie.
Die wissenschaftliche und mathematische Bedeutung dieser enormen Zahlen liegt in ihrer Fähigkeit, Konzepte wie Unendlichkeit und das Wachstum von Potenzen zu veranschaulichen. Sie bieten eine Plattform, auf der Mathematiker die Grenzen des Zählbaren und der Zahlentheorie erforschen können. In der Mathematik sind Zahlen grundsätzlich unendlich, was bedeutet, dass es immer eine Zahl gibt, die noch gröer ist als jede zuvor definierte Zahl.
Anwendung grosser Zahlen in der realen Welt
Grosse Zahlen begegnen uns nicht nur in der Theorie, sondern auch praktisch in vielen Bereichen des Alltags, der Wissenschaft und der Wirtschaft. In der Astronomie zum Beispiel sind grosse Zahlen allgegenwärtig, wenn es um Entfernungen zwischen Sternen und Galaxien geht, die in Lichtjahren gemessen werden. Ein Lichtjahr entspricht etwa zehn Billionen Kilometern – eine Zahl, die ohne das Konzept der Zehnerpotenzen und ohne das Umrechnen der Masseinheiten schwer zu begreifen wäre.
Zehnerpotenzen sind eine praktische Art, sehr grosse oder sehr kleine Zahlen darzustellen. Sie verwenden die Basis 10 und eine Hochzahl (Exponent), um zu zeigen, wie oft die 10 multipliziert oder dividiert wird.
Positive Exponenten: Eine Zehnerpotenz mit einem positiven Exponenten bedeutet, dass die 10 mehrfach miteinander multipliziert wird.
Bsp: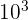 
bedeutet 10x10x10=1000.
Negative Exponenten: Eine Zehnerpotenz mit einem negativen Exponenten bedeutet, dass die 10 mehrfach geteilt wird.
Bsp: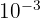 
bedeutet 1/10x10x10=0,001
Zehnerpotenzen machen es einfacher, mit sehr grossen oder sehr kleinen Zahlen zu arbeiten, ohne viele Nullen zu schreiben.
In der Umweltforschung helfen grosse Zahlen, die Populationen von Spezies oder die Menge von Molekülen in einem bestimmten Volumen Luft zu quantifizieren, was für das Verständnis von Ökosystemen und Klimaveränderungen unerlässlich ist. Hierbei werden oft Zahlen in den Grössenordnungen von Billiarden verwendet, um die immense Anzahl natürlicher Vorgänge zu beschreiben.
In der Volkswirtschaft sind grosse Zahlen ebenfalls unverzichtbar. Die Berechnung des Bruttoinlandsprodukts eines Landes oder die Bewertung von Märkten und deren Kapazitäten erfordert das Verständnis und den Umgang mit Millionen, Milliarden und Trillionen. Diese Zahlen helfen Ökonomen, die wirtschaftliche Leistung und Trends zu analysieren und zu verstehen.
Die Fähigkeit, grosse Zahlen zu begreifen und mit ihnen zu rechnen, ist daher nicht nur eine akademische Übung, sondern eine notwendige Fertigkeit, um komplexe, globale Herausforderungen in Wissenschaft und Wirtschaft zu meistern. Sie springen aus den Lehrbüchern direkt in die Realität, wo sie helfen, unsere Welt zu messen, zu verstehen und zu verwalten.
Häufige Fehler und Missverständnisse
Im Umgang mit grossen Zahlen treten häufig Fehler und Missverständnisse auf, die es zu vermeiden gilt. Ein klassischer Fehler ist das Übersehen der Bedeutung von Stellen und Ziffern. Beispielsweise wird oft nicht beachtet, wie signifikant eine einzige Ziffer in einer grossen Zahl sein kann, besonders wenn es sich um Milliarden oder Billionen handelt. Ein weiteres Missverständnis ist die Verwechslung von metrischen Vorsätzen, wie "Mio" für Million und "Bio" für Billion, was zu erheblichen Fehlinterpretationen führen kann.
Um solche Fehler zu vermeiden, ist es wichtig, die Prinzipien der Stellenwerttafel zu verstehen und konsequent anzuwenden. Das gründliche Erlernen und regelmässige Üben Verständnis grosser Zahlen kann helfen, diese Fehler zu minimieren. Zudem sollten Schüler und Studierende darauf trainiert werden, die Bedeutung jeder Ziffer innerhalb einer grossen Zahl genau zu überprüfen und die metrischen Präfixe korrekt zu verwenden.
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
