Wenn wir in der Grundschule anfangen, Mathematik zu lernen, um zu zählen und zu rechnen, legen wir damit unwissentlich einen ganz wesentlichen Grundstein. Die Mathematik gilt als die Wissenschaft der Präzision und Logik, doch selbst in dieser scheinbar perfekten Welt gibt es Rätsel, die bis heute niemand lösen konnte.
Einige mathematische Probleme wurden nie gelöst! Selbst die grössten Forscher haben keine Lösung gefunden! Sie sind nicht nur Denksport für Genies, sondern auch Schlüssel zu neuen Erkenntnissen, die unser Verständnis der Welt revolutionieren könnten.
Superprof stellt Dir die Probleme vor, die in der Mathematik nie gelöst wurden und drückt die Daumen, dass Du eines Tages Teil der fabelhaften Welt der Mathematik werden wirst und es schaffst, eines dieser Probleme zu lösen!
Die Riemannsche Hypothese
Dieses Problem wird von vielen Mathematikern als eines der schwierigsten aller Zeiten angesehen. Die Hypothese fasziniert Forscher seit über 160 Jahren und wurde dennoch nie geklärt.
Sie wurde 1859 von dem deutschen Mathematiker Bernhard Riemann formuliert und beschäftigt sich mit der Verteilung der Primzahlen – den Bausteinen aller natürlichen Zahlen. Obwohl Primzahlen wie 2, 3, 5, 7 oder 11 auf den ersten Blick unregelmässig verteilt erscheinen, vermutet die Riemannsche Hypothese eine tiefere, verborgene Ordnung in ihrem Auftreten.
Schau Dir die Riemannsche Hypothese im Video an:
Riemanns Vermutung basiert auf der sogenannten Riemannschen Zeta-Funktion – einer mathematischen Funktion, die unendlich viele Werte hat. Die Riemannsche Hypothese besagt, dass alle nicht-trivialen Nullstellen der Zeta-Funktion – also die Werte, für die die Funktion null wird – auf einer bestimmten geraden Linie in der komplexen Zahlenebene liegen.
Er setzte damit die Arbeit seines Professors Carl Friedrich Gauss fort und bewies die sogenannte Funktionalgleichung der Zetafunktion:
- Er bewies eine gewisse Symmetrie-Eigenschaft bzgl. des Punktes s = 1/2
- Gab explizite Formeln an, welche die Funktion pi(x), die die Primzahlen <= x zählt, mit den nicht-reellen Nullstellen der Zetafunktion verbinden.
- Dabei stellte er die Vermutung auf, dass diese sog. nicht-trivialen Nullstellen alle den Realteil 1/2 haben.
Er kommentiert:
Hierfür wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen.
Bernhard Riemann
Mittlerweile wurde das Problem vom Clay Mathematics Institute in die Liste der "Millennium-Probleme" aufgenommen. Derjenige, der die Hypothese belegen kann, gewinnt eine Million US-Dollar.
Auch wenn die Funktionalgleichung in der Mathematik bewiesen ist, ist die Hypothese Teil der Liste für unlösbare Matheaufgaben.
Die Hodge-Vermutung
Die Vermutung von Hodge gehört ebenfalls zu den sieben vom Clay Institute im Jahr 2000 definierten Millennium-Problemen. Sie verbindet die Welt der algebraischen Geometrie mit der Topologie und ist für Mathematiker ein entscheidendes Puzzle, um die Struktur höherdimensionaler geometrischer Objekte besser zu verstehen.
Die Hodge-Vermutung, die 1950 von Sir William Vallance Douglas Hodge formuliert wurde, stellt eine faszinierende Frage: Lassen sich alle bestimmten topologischen Eigenschaften algebraischer Varietäten durch algebraische Objekte beschreiben?
Seine Vermutung besagt, dass die algebraischen Zyklen von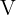 
den gesamten Raum 
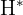aufspannen. Das bedeutet, dass die angegebenen Bedingungen, die notwendig für eine Kombination algebraischer Zyklen sind, auch hinreichend sind.
Klingt ziemlich komplex, oder? Konkret bedeutet das folgendes:
Können bestimmte Zyklen (geschlossene geometrische Formen) in der Topologie einer Varietät durch algebraische Gleichungen beschrieben werden?
Algebraischen Zyklen = sichtbare Teile der Varietät (durch Polynome definiert)
topologische Zyklen = umfassen alle möglichen geschlossenen Formen die in der Struktur existieren
Die preisgekrönte französische Mathematikerion Claire Voisin, Goldmedaillengewinnerin am CNRS, arbeitet zur Zeit an dieser Hypothese. Ihrer Ansicht nach wäre ihre Demonstration ein wahrer mathematischer Schatz.
Hier braucht es tiefergehende Kenntnisse, um die Aufgaben der Mathematik lösen!
Die Vermutung von Birch und Swinnerton-Dyer
Bei der Birch- und Swinnerton-Dyer-Vermutung handelt es sich um algebraische Gleichungen, die Du während Deines Mathematikunterrichts sicher gelernt hast. Du wirst jedoch ein bestimmtes Niveau in Mathematik benötigen, bevor Du versuchen kannst, das Problem zu lösen.
Die Vermutung sagt etwas über den Rang elliptischer Kurven aus. Es ist bereits recht kompliziert, die Lösungen einer Polynomgleichung P (x, y) = 0 zu bestimmen, wobei x und y rationale Zahlen wären.
Das Verhalten der L-Funktion an einer bestimmten Stelle gibt Auskunft darüber, wie viele Lösungen eine elliptische Kurve besitzt.
Die L-Funktion ist ein analytisches Objekt, das aus der elliptischen Kurve abgeleitet wird. Die Vermutung von Birch und Swinnerton-Dyer stellt einen Zusammenhang zwischen der Rang der elliptischen Kurve (die Anzahl der unabhängigen rationalen Punkte auf der Kurve) und dem Verhalten der L-Funktion bei einem bestimmten Punkt, nämlich bei s=1, her.
Die Vermutung basiert darauf, dass der Rang nur von der gegebenen Anzahl von Lösungen der Gleichung für eine Primzahl P abhängt.
Die Navier-Stoke-Gleichung
Die Gleichung ist eines der bedeutendsten und gleichzeitig eines der schwierigsten Probleme in der Mathematik und Physik. Hier geht es um die Physik und die Mechanik von Flüssigkeiten.
Weniger bekannt als E = MC2, zielt die Navier-Stoke-Gleichung, die sowohl Physiker als auch Mathematiker fasziniert, darauf ab, die Bewegung von Flüssigkeiten oder genauer ihr Geschwindigkeitsfeld zu beschreiben.
Mathematisch ausgedrückt ist die Navier-Stokes-Gleichung eine partielle Differentialgleichung, die die Geschwindigkeit und den Druck eines Fluids in Bezug auf die Zeit und den Raum beschreibt. Sie berücksichtigt verschiedene Faktoren wie Viskosität, Dichte und Beschleunigung des Fluids.
Es handelt sich um eine nichtlineare Differentialgleichung, die sehr oft verwendet wird, ihre Lösung wurde allerdings noch nicht gefunden! Sie dient auch dazu, die Bewegungen der Strömungen in den Ozeanen besser zu verstehen.
Hier spielen zwei Fragen eine Rolle:
- Existenz: Gibt es immer eine Lösung für die Navier-Stokes-Gleichung? Insbesondere für beliebige Anfangsbedingungen und in allen möglichen Umgebungen (in beliebig hohen Dimensionen)?
- Regularität: Sind die Lösungen der Gleichung immer glatt? Das heisst, sind die Geschwindigkeitsfelder des Fluids immer differenzierbar und ohne Unstetigkeiten, auch bei extremen Bedingungen wie Turbulenzen?
Der Nachweis der Navier-Stoke-Gleichung bringt den berühmten Clay Institute-Preis, denn auch sie gehört zu den sieben Millennium-Problemen.
Suchst du nach Mathematik Nachhilfe Winterthur? Mit Superprof findest du die passende Lehrkraft!
Die Yang Mills Gleichungen
Die Yang-Mills-Gleichungen sind ein zentrales Konzept in der theoretischen Physik und Mathematik, die die Grundlage für viele moderne Theorien, einschliesslich der Quantenfeldtheorie und der Teilchenphysik, bilden.
Das folgende Problem wurde bereits bewiesen:
Sie wurden in den 1950er Jahren von den Physikern C. N. Yang und Robert Mills formuliert und beschreiben die Wechselwirkungen von Feldern, die durch sogenannte Gauge-Symmetrien bestimmt werden.
Mathematisch gesehen sind die Yang-Mills-Gleichungen ein System von nichtlinearen partiellen Differentialgleichungen, die die Dynamik von Gauge-Feldern und deren Wechselwirkungen mit Materie beschreiben.
Übrigens: Gauge-Symmetrien sind mathematische Transformationen, die die physikalischen Felder in einer bestimmten Art und Weise verändern, ohne die beobachtbaren physikalischen Eigenschaften zu beeinflussen.
Um das unendlich Kleine zu erklären, versuchten Yang und Mills, Elementarteilchen zu beschreiben, indem sie ein Modell konstruierten, das auf geometrischen Theorien basierte. Folgende Theorien basieren auf den Yang-Mills-Gleichungen:
Quantenchromodynamik
Elektroschwache Wechselwirkung
Ihre Theorie, wonach bestimmte Quantenteilchen eine positive Masse haben, wurde durch zahlreiche Computersimulationen bestätigt. Experimentell wurde dies von den beiden Physikern entdeckt, aber aus theoretischer Sicht ist es immer noch nicht belegt.
Suchst du nach Mathe Nachhilfe Zug? Mit Superprof findest du die passende Lehrkraft!
P = NP Problem
Dieses Jahrtausendproblem ist sicherlich eines der wichtigsten von allen! Aus seiner Lösung würde sich die Lösung anderer Probleme ergeben, während das Gegenteil implizieren würde, dass sie sicherlich für immer ungelöst bleiben werden ...
Es wurde von Stephen Cook 1971 in seiner Arbeit über die Komplexität von Entscheidungsproblemen formuliert und stellt seitdem eines der zentralen ungelösten Rätsel der Mathematik dar. Es beschäftigt sich mit einer grundlegenden Frage in der Theoretischen Informatik: Können Probleme, deren Lösungen schnell überprüft werden können, auch schnell gelöst werden?
Zunächst gilt:
P (polynomielle Zeit) = Entscheidungsprobleme, die in polynomieller Zeit gelöst werden können
NP (nichtdeterministische polynomielle Zeit = Entscheidungsprobleme, bei denen, wenn eine Lösung gegeben ist, diese in polynomieller Zeit überprüft werden kann
Was also besagt das Problem:
Alle Probleme in P sind auch in NP, da eine Lösung, die in polynomieller Zeit gefunden wird, natürlich auch in polynomieller Zeit überprüft werden kann. Die Frage ist aber: Ist P gleich NP?
In engem Zusammenhang mit der Funktionsweise von Computern und Algorithmen, könnten wir dieses Problem wörtlich durch die folgende Frage übersetzen: Können wir dank einer intelligenten Berechnung das herausfinden, was wir herausfinden können, indem wir einfach Glück haben?
Auch auf diese Frage gibt es noch keine Antwort. Auch dieses Problem ist eines der Millennium-Probleme, für deren Lösung das Clay Mathematics Institute im Jahr 2000 eine Belohnung von 1 Million US-Dollar ausgelobt hat.
Wie wäre es mit Nachhilfe Mathematik Baden?
Der Satz von Ramsey
Benannt nach dem britischen Mathematiker Frank P. Ramsey, beschreibt der Satz die Bedingungen, unter denen in bestimmten Strukturen zwangsläufig bestimmte Muster oder Teilstrukturen vorkommen.
Wenn man ein ausreichend grosses System von Objekten hat, wird es immer einen Teil davon geben, der ein bestimmtes, geordnetes Muster aufweist.
Ramseys Theorem ist mit der Suche nach Ordnungen und Modellen innerhalb von Systemen verknüpft.
Nach dieser Theorie gibt es keine vollständige Unordnung. Schau dir die beiden Beispiele an:
- Wenn wir die Punkte n auf einem Blatt Papier zeichnen und jeder Punkt durch eine rote oder blaue Linie mit allen anderen Punkten verbunden ist, muss n gleich 6 sein, um sicherzustellen, dass mindestens ein blaues oder ein rotes Dreieck vorhanden ist.
- Einfacher könnte man auch fragen, wie gross eine Gruppe sein muss, damit mindestens drei Personen Ausländer sind und drei von ihnen sich gegenseitig kennen. Die Lösung für dieses Problem ist 6.
Wenn Du jedoch die Zahl drei durch vier änderst, ist das Problem nicht zu lösen.
Zumindest hat es heute kein Mathematiker geschafft.
Wenn wir über unlösbare Matheaufgaben sprechen, darf der Satz von Ramsey nicht fehlen.
Suchst Du nach Nachhilfe Mathematik Oberstufe? Finde die passende Lehrkraft auf Superprof!
Die Zahlen von Lychrel und die Palindrome
In der Welt der Zahlen gibt es viele faszinierende Phänomene, eines davon ist das Rätsel der Lychrel-Zahlen. Diese Zahlen sind eng mit der Idee der Palindrome verbunden, einer besonderen Art von Zahlen, die sich vorwärts und rückwärts gleich lesen lassen (17371 ist zum Beispiel ein Palindrom).
Eine Lychrel-Zahl ist eine Zahl, die – wenn man wiederholt ihre Ziffern umkehrt und die resultierende Zahl zu der ursprünglichen Zahl hinzufügt – niemals ein Palindrom bildet.
Wenn ein Palindrom wiederholt mit seiner Umkehrung addiert wird und das Ergebnis keine Palindromzahl ergibt, dann ist es eine Lychrelzahl.
- 59 ist keine Lychrelzahl, weil:
- 59 + 95 = 154
- 154 + 451 = 605
- 605 + 506 = 1111
- Wir landen bei einem Palindrom.
Die kleinste Zahl, für die kein Palindrom gefunden wurde, ist 196, Trotz vieler Jahre der Berechnungen hat niemand ein Palindrom für 196 gefunden, egal wie oft der Lychrel-Prozess angewendet wurde. Selbst nach mehr als zwölf Millionen wiederholten Additionen (natürlich mittels Computerprogrammen) hat man für die Zahl 196 noch kein Palindrom gefunden! Genau das begeistert jeden Mathematiker!
Die genaue Definition einer Lychrel-Zahl ist jedoch noch nicht abschliessend geklärt, da es keine mathematische Garantie gibt, dass eine Zahl niemals ein Palindrom bilden kann. Es gibt jedoch Vermutungen und Beobachtungen, die darauf hindeuten, dass einige Zahlen tatsächlich niemals ein Palindrom erzeugen.
Nun kennst Du einige der Millennium-Probleme der Mathematik.
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
