Der Goldene Schnitt, auch „goldener Anteil“ genannt, beschreibt ein einzigartiges Verhältnis: Der kleinere Teil verhält sich zum grösseren Teil wie der grössere Teil zur gesamten Strecke. Mathematisch wird dies durch die Formel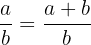 
dargestellt.
Dieses Verhältnis ergibt die irrationale Zahl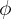 
(Phi), die ungefähr 1,6181 beträgt. Der Goldene Schnitt ist nicht nur mathematisch faszinierend, sondern findet sich auch in Kunst, Architektur und der Natur. Achtung! Phi ist nicht zu verwechseln mit der Zahl Pi.
Die Geschichte des goldenen Schnitts
Der Goldene Schnitt hat eine lange Geschichte und war schon in der Antike bekannt, insbesondere bei den Pythagoräern. Sie nutzten ihn in der Geometrie, beispielsweise beim Bau von Pentagons mit gleichschenkligen Dreiecken.
Damals betrachteten die Pythagoräer den Goldenen Schnitt jedoch nicht in arithmetischer Weise, da sie irrationale Zahlen wie den Goldenen Schnitt philosophisch ablehnten und nur rationale Zahlen akzeptierten.
Der erste schriftliche Nachweis über den Goldenen Schnitt stammt von Euklid (300 v. Chr.) in seinem Werk Elemente. Er beschreibt: „Eine Strecke wird durch einen Punkt so geteilt, dass sich der grössere Abschnitt zur Strecke verhält wie der kleinere Abschnitt zum grösseren.“ Diese Teilung definiert den Goldenen Schnitt, das Verhältnis der Teilstrecken wird später als „Goldene Zahl“ bezeichnet.
Obwohl Platon ebenfalls Geometrie und Proportionen intensiv untersuchte, gibt es keine eindeutigen Hinweise, dass er den Goldenen Schnitt explizit als Forschungsgegenstand behandelte. Zu dieser Zeit war die Bezeichnung „Goldene Zahl“ noch nicht gebräuchlich.
Eine andere interessante Zahl ist die eulersche Zahl e.
Die goldene Zahl im Mittelalter
Im Mittelalter erfuhr der Goldene Schnitt neue Aufmerksamkeit. Der persische Mathematiker Al-Khwarizmi untersuchte im 8. Jahrhundert verschiedene Methoden zur Teilung einer Länge von zehn Einheiten in zwei Abschnitte. Eine seiner Lösungen entspricht dem Verhältnis des Goldenen Schnitts, auch wenn er diesen Begriff nicht verwendete.
Leonardo Fibonacci, einer der einflussreichsten Mathematiker des Mittelalters, brachte Al-Khwarizmis Gleichungen nach Europa. Obwohl Fibonacci durch seine berühmte Zahlenfolge indirekt eine Verbindung zum Goldenen Schnitt herstellte, erkannte er selbst keinen expliziten Zusammenhang.
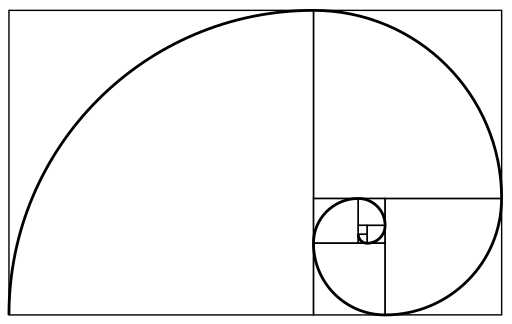
Die Irrationalität des Goldenen Schnitts wurde im 13. Jahrhundert von Campanus von Novara, einem italienischen Mathematiker und Astronomen, untersucht. Er zeigte dies unter anderem anhand des Prinzips des unendlichen Abstiegs, das in der Goldenen Spirale sichtbar wird.
Suchst du nach Mathematik Nachhilfe Winterthur? Mit Superprof findest du die passende Lehrkraft!
Die goldene Zahl in der Renaissance
In der Renaissance wird die Goldene Zahl als göttliches Verhältnis bezeichnet und gilt als göttliche Intervention gemäss dem Buch des italienischen Mathematikers Luca Parioli "Summa de Arithmetica, Geometria, Proportioni et Proportionalità", das von Leonardo da Vinci illustriert wird.
Zu dieser Zeit entsteht auch die Verbindung zwischen Fibonacci und dem Goldenen Schnitt. Durch Teilen eines Terms in der Sequenz durch den vorherigen Term, kommt das Ergebnis dem Goldenen Schnitt nahe. Die Annäherung ist umso besser, je höher der Term ist.
Diese Beziehung wird in einer anonymen Notiz beschrieben und das Ergebnis wird tatsächlich von dem deutschen Mathematiker Johannes Kepler bewiesen, der sein ganzes Leben lang von der Goldenen Zahl fasziniert sein wird. Sie ist für ihn das "Juwel der Geometrie" und von grösserer Bedeutung als andere besondere Zahlen.
Die Geburt eines Mythos im neunzehnten Jahrhundert
Die Zahl verliert ihre mathematische Bedeutung, gewinnt aber als System zunehmend an Interesse. Der deutsche Philosoph Adolf Zeising glaubt, dass der Goldene Schnitt dazu beitragen kann, sowohl wissenschaftliche als auch künstlerische Konzepte zu begreifen.
Trotz eines zweifelhaften wissenschaftlichen Ansatzes, sind die Theorien von Zeisig sehr attraktiv. Dank des Goldenen Schnitts könne man Schönheit erklären. Auch im 20. Jahrhundert fasziniert die Goldene Zahl noch Mathematiker, Künstler und Architekten.
Kleine Info am Rande: Wenn Du Mathe-Liebhaber bist, hat für Dich bestimmt jede Zahl was perfektes, da Du von Zahlen fasziniert bist. Es gibt jedoch tatsächlich eine Zahl, die sich wirklich so nenn: Perfekte Zahl.
Die goldene Zahl in der Geometrie
Der Goldene Schnitt ist nicht nur mathematisch bemerkenswert, sondern hat auch eine besondere ästhetische Wirkung. In der Natur findet sich dieses Verhältnis oft, weil es Strukturen ermöglicht, die sowohl stabil als auch effizient sind. Beispiele dafür sind Spiralen in Schneckenhäusern, Blätteranordnungen bei Pflanzen und die Symmetrie von Fünfecken.
In der Geometrie bildet der Goldene Schnitt die Grundlage für Formen wie das Pentagon und das Goldene Rechteck, die wiederum harmonische Proportionen erzeugen. Diese Eigenschaften machen den Goldenen Schnitt zu einem universellen Prinzip, das Mathematik, Natur und Kunst verbindet.
Die erste Definition des Goldenen Schnitts ist geometrisch.
Der Satz lautet wie folgt:
"Zwei Längen a und b (streng positiv) berücksichtigen den 'Goldenen Anteil', wenn das Verhältnis von a zu b gleich dem Verhältnis von a + b zu a ist."
Im Lichte der Arbeit von Euklid erscheint eine neue Definition der Goldenen Zahl:
"Die Goldene Zahl ist die positive reelle Zahl, die mit 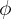bezeichnet wird und dem Bruch 
entspricht, wenn a und b zwei Zahlen im Verhältnis von extremem und durchschnittlichem Grund sind."
Hier ist die entsprechende Formel dazu: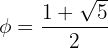 
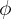ist die Lösung einer Gleichung zweiten Grades, die eine dritte Definition ergibt:
"Der Goldene Schnitt ist die einzige Lösung für die Gleichung 
"
(Die besondere Zahl Null lohnt es sich übrigens auch, im Einzelnen zu betrachten!)
Dank dieser Berechnungen ist es möglich, mithilfe eines Kompasses, eines Lineals und eines Geodreiecks eine Proportion mit mittlerem und extremem Verhältnis zu zeichnen:
- Zeichne einen Kreis C mit Radius 1.
- Zeichne am Ende des Radius 1 ein Segment der Länge
senkrecht zum Radius. - Zeichne den Kreis C 'mit dem Radius , indem Du die Kompassspitze am Ende des zuvor gezeichneten Abschnitts mit der Länge platzierst.
- Zeichne das Segment von der Mitte des Kreises C bis zum Ende des Kreises C 'durch die Mitte des Kreises C'.
- Die Länge dieses Segments ist der goldene Schnitt.
Anhand dieser Kreise ist es möglich, ein goldenes Rechteck zu zeichnen.
Wir können auch eine quadratische Seite a - b in das goldene Rechteck der Seiten b × (a - b) integrieren. Durch Hinzufügen eines Viertelkreises in jedes Quadrat erhalten wir eine Spirale, die als "Goldene Spirale" bezeichnet wird.
Der Goldene Schnitt kann auch für die Konstruktion von Pentagonen und Pentagrammen sowie für die Trigonometrie verwendet werden.
Suchst du nach Mathematik Nachhilfe Zug? Mit Superprof findest du die passende Lehrkraft!
Der goldene Schnitt in der Arithmetik
Neben der geometrischen Darstellung lässt sich der Goldene Schnitt auch algebraisch definieren. Algebraisch ist der Goldene Schnitt 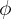die einzige positive Lösung der Gleichung . Alternativ kann man ihn durch die Gleichung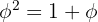 
beschreiben, die ebenfalls den besonderen Zusammenhang zwischen 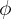und seinen Potenzen verdeutlicht.
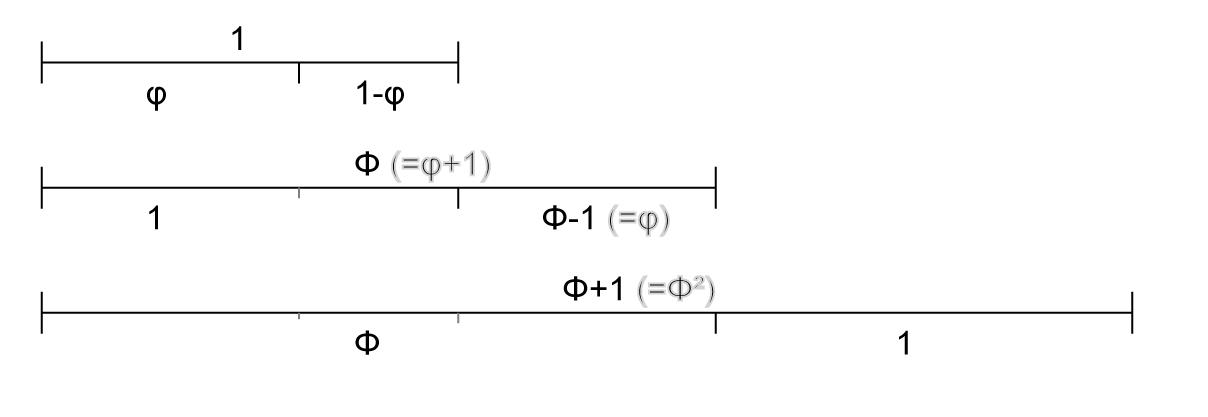
Der Goldene Schnitt lässt sich ausserdem durch eine Kettenbruchdarstellung annähern:
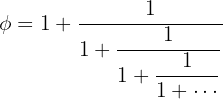
Diese Darstellung zeigt, dass 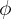eine irrationale Zahl ist, die sich durch unendliche wiederkehrende Muster auszeichnet.
Die Fibonacci-Zahlen sind eine Folge von Zahlen, bei der jede Zahl die Summe der beiden vorhergehenden Zahlen ist. Die Folge beginnt mit den Zahlen 0 und 1 und sieht so aus:
0,1,1,2,3,5,8,13,21,34,...
Die Formel zur Berechnung einer Fibonacci-Zahl lautet: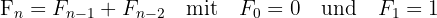
Ein weiterer Zusammenhang besteht mit der Fibonacci-Folge: Das Verhältnis aufeinanderfolgender Fibonacci-Zahlen nähert sich mit zunehmender Grösse der Zahlen dem Wert des Goldenen Schnitts immer weiter an. Umgekehrt wird die Fibonacci-Folge durch die sogenannte Formel von Binet berechnet, die den Goldenen Schnitt direkt einbezieht:
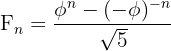
Zur Algebra gehört im Übrigen auch eine andere besondere Zahl, nämlich die imaginäre Zahl i. Ja, richtig gehört ZAHL und nicht Buchstabe.
Die Allgegenwart des goldenen Schnitts
Wie Du sicher gemerkt hast, ist der Goldene Schnitt in der Mathematik allgegenwärtig, aber auch überall um uns herum.
Auch in der Natur finden wir den Goldenen Schnitt:
- Die Schuppen eines Tannenzapfens erzeugen logarithmische Spiralen, die der Fibonacci-Folge entsprechen können.
- Die Staubblätter einer Sonnenblume erzeugen das gleiche Phänomen,
- Quarzkristalle präsentieren in einem fünfeckigen Muster den Goldenen Schnitt,
- Die Rinde einer Ananas bringt ebenfalls eine Fibonacci-Spirale hervor, die mit dem Goldenen Schnitt verwandt ist.
Manche Menschen wollen dahinter ein mystisches oder göttliches Phänomen erkennen - vielleicht ist es aber auch nur reiner Zufall...
Suchst Du nach Nachhilfe Mathematik Oberstufe? Finde die passende Lehrkraft auf Superprof!
Der goldene Schnitt im Menschen?
Die Frage, ob der menschliche Körper mit dem Goldenen Schnitt verbunden ist oder nicht, wurde wiederholt gestellt, sei es von wissenschaftlicher, künstlerischer oder ästhetischer Seite.
Zeising hatte versucht, den menschlichen Körper nur anhand des Goldenen Schnittes zu messen, aber dieser Versuch wurde bald aufgegeben. Die auf diese Weise gezeichneten Proportionen des menschlichen Körpers waren nicht realistisch.
Darüber hinaus ändern sich die Dimensionen des menschlichen Körpers ständig. Der Mensch wächst mit der Evolution und nicht unbedingt auf einheitliche Weise.
Die Suche nach dem Goldenen Schnitt beim Menschen wurde jedoch nicht aufgegeben. Heute untersuchen Wissenschaftler ob es in unserem Gehirn eventuell einen Zusammenhang mit dem Goldenen Schnitt geben könnte. Diese Theorie bleibt jedoch umstritten.
Der Goldene Schnitt wird oft als besonders harmonisch und angenehm wahrgenommen, da sein Verhältnis in der Natur und in menschlichen Kreationen häufig vorkommt. Unser Gehirn scheint solche Proportionen intuitiv zu bevorzugen, da sie für Balance und Symmetrie stehen.
Künstler und Architekten nutzen den Goldenen Schnitt bewusst, um Werke zu schaffen, die visuell ansprechend wirken. Dies zeigt sich in berühmten Gemälden wie der „Mona Lisa“ oder Bauwerken wie dem Parthenon. Selbst moderne Studien deuten darauf hin, dass der Goldene Schnitt ein universelles Prinzip für Ästhetik und Wahrnehmung sein könnte.
Die goldene Zahl in den bildenden Künsten und Architektur
Der Goldene Schnitt fasziniert nicht nur die Wissenschaftler, sondern auch in vielen anderen Bereichen wie der Malerei, insbesondere in der Renaissance.
Wir finden ihn zum Beispiel im Gemälde "Die Geburt der Venus" von Botticelli, aber auch in der "Mona Lisa" von Leonardo da Vinci.
Aber manchmal sind es auch spätere Interpretationen und kein Wille des Künstlers - wie das Gemälde "Heiliger Hieronymus" von Leonardo da Vinci nahe legt.
Ebenso ist die Verwendung des Goldenen Schnitts in alten Bauten umstritten. Es ist schwer zu sagen, ob die Erbauer sich der Verwendung des Goldenen Schnitts bewusst waren oder ob es sich um eine Überinterpretation der Archäologen handelt.
Es gibt mehrere Beispiele:
- Das Theater von Epidaurus,
- Die grosse Pyramide von Gizeh
- Die Symmetrie der Fassade des Parthenon,
- Der Turm von Methoni,
- Der grosse Pergamon-Altar.
Der französische Architekt Le Corbusier entwickelte in den Jahren 1942 bis 1955 ein System namens Modulor, ein Proportionssystem, das den bedeutendsten modernen Versuch darstellt, der Architektur eine am Mass des Menschen orientierte mathematische Ordnung zu geben. Er verwendete sein System in vielen seiner Bauten wie der avantgardistischen Cité Radieuse in Marseille oder der Kapelle Notre Dame du Haut von Ronchamp.
Auch in der Musik stossen wir auf den Goldenen Schnitt und zwar in zwei Formen:
Zum einen können zwei Töne bzw. ihre Frequenzen zueinander in der Proportion des Goldenen Schnittes stehen. Andererseits kann die Komposition eines Stückes aus Teilen bestehen, deren Längen sich zueinander verhalten wie der Goldene Schnitt.
Und wir könnten noch lange fortfahren, da der Goldene Schnitt viele Menschen fasziniert und Gegenstand vieler mehr oder weniger wissenschaftlicher Theorien ist! Und danach gibt es noch viele weitere interessante besondere Zahlen in der Mathematik, wie die Primzahlen zum Beispiel. Dazu aber mehr in extra Artikeln. Wir wollen ja nicht übertreiben?
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
